Orthogonal polynomials
In mathematics, an orthogonal polynomial sequence is an infinite sequence of real polynomials
of one variable x, in which each pn has degree n, and such that any two different polynomials in the sequence are orthogonal to each other under a particular version of the L2 inner product.
The field of orthogonal polynomials developed in the late 19th century from a study of continued fractions by P. L. Chebyshev and was pursued by A.A. Markov and T.J. Stieltjes and by a few other mathematicians. Since then, applications have been developed in many areas of mathematics and physics.
Definition
The theory of orthogonal polynomials includes many definitions of orthogonality. In abstract notation, is convenient to write
when the polynomials p(x) and q(x) are orthogonal. A sequence of orthogonal polynomials, then, is a sequence of polynomials
such that pn has degree n and all distinct members of the sequence are orthogonal to each other.
The algebraic and analytic properties of the polynomials depend upon the specific assumptions about the operator  . In the classical formulation, the operator is defined in terms of the integral of a weighted product (see below) and happens to be an inner product. Other formulations remove various assumptions, for example in the context of Hilbert spaces or non-Hermitian operators (see below). Most of the discussion in this article applies to the classical definition.
. In the classical formulation, the operator is defined in terms of the integral of a weighted product (see below) and happens to be an inner product. Other formulations remove various assumptions, for example in the context of Hilbert spaces or non-Hermitian operators (see below). Most of the discussion in this article applies to the classical definition.
Classical formulation
Let ![[x_1, x_2]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/48f0a3fbaaf45d915fd69980c25b8d48.png) be an interval in the real line (where
be an interval in the real line (where 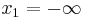 and
and 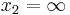 are allowed). This is called the interval of orthogonality. Let
are allowed). This is called the interval of orthogonality. Let
be a function on the interval, that is strictly positive on the interior 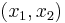 , but which may be zero or go to infinity at the end points. Additionally, W must satisfy the requirement that, for any polynomial
, but which may be zero or go to infinity at the end points. Additionally, W must satisfy the requirement that, for any polynomial 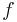 , the integral
, the integral
is finite. Such a W is called a weight function.
Given any  ,
,  , and W as above, define an operation on pairs of polynomials f and g by
, and W as above, define an operation on pairs of polynomials f and g by
This operation is an inner product on the vector space of all polynomials. It induces a notion of orthogonality in the usual way, namely that two polynomials are orthogonal if their inner product is zero.
Generalizations
Many alternative theories of orthogonal polynomials have been studied and, along with the classical theory, remain active areas of research.[1] Some aspects of the classical theory generalize when certain assumptions are lifted, and new properties can arise in different contexts.
In some theories the polynomials may act on other algebraic objects such as the complex numbers, matrices, and the unit circle (as a subset of the complex numbers).
Much of the general theory is for operators  that satisfy the axioms of an inner product. This includes inner products within a Hilbert space (where the polynomials can be interpreted as an orthogonal basis) and inner products that can be defined as an integral of the form
that satisfy the axioms of an inner product. This includes inner products within a Hilbert space (where the polynomials can be interpreted as an orthogonal basis) and inner products that can be defined as an integral of the form
where μ is a positive measure; this in turn includes the classical definition as well as the probabilistic definition (where the measure is a probability measure) and the discrete definition (where the integral is an infinite weighted sum).
The effects of lifting the inner product assumption of positive definiteness have also been studied (e.g. negative weights, discrete coefficients or non-Hermitian operators). In this theory, the terms system and sequence of orthogonal polynomials are distinct because pairs of polynomials of the same degree may be orthogonal.
For the remainder of this article the classical definition is assumed.
Standardization
The chosen inner product induces a norm on polynomials in the usual way:
When making an orthogonal basis, one may be tempted to make an orthonormal basis, that is, one in which all basis elements have norm 1. For polynomials, this would often result in simple square roots in the coefficients. Instead, polynomials are often scaled in a way that mathematicians agree on, that makes the coefficients and other formulas simpler. This is called standardization. The "classical" polynomials listed below have been standardized, typically by setting their leading coefficients to some specific quantity, or by setting a specific value for the polynomial. This standardization has no mathematical significance; it is just a convention. Standardization also involves scaling the weight function in an agreed-upon way.
Denote by 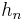 the square of the norm of
the square of the norm of  :
:
The values of 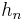 for the standardized classical polynomials are listed in the table below. In this notation,
for the standardized classical polynomials are listed in the table below. In this notation,
where δmn is the Kronecker delta.
Example: Legendre polynomials
The simplest classical orthogonal polynomials are the Legendre polynomials, for which the interval of orthogonality is [−1, 1] and the weight function is simply 1:
These are all orthogonal over [−1, 1]; whenever m ≠ n,
The Legendre polynomials are standardized so that Pn(1) = 1 for all n.
Non-classical example
The simplest non-classical orthogonal polynomials are the monomials
for n ≥ 0 which are orthogonal under the inner product defined by
This inner product cannot be defined in the classical sense as a weighted integral of a product, or even as a measure of a product (otherwise 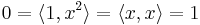 ). However the monomials are orthogonal on the unit circle as a subset of the complex numbers, using the path integral
). However the monomials are orthogonal on the unit circle as a subset of the complex numbers, using the path integral
where 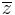 is the complex conjugate of
is the complex conjugate of  . The properties of orthogonal polynomials on the unit circle differ from those of classical orthogonal polynomials (such as the form of the recurrence relations and the distribution of roots) and are related to the theory of Fourier series.
. The properties of orthogonal polynomials on the unit circle differ from those of classical orthogonal polynomials (such as the form of the recurrence relations and the distribution of roots) and are related to the theory of Fourier series.
General properties of orthogonal polynomial sequences
All orthogonal polynomial sequences have a number of elegant and fascinating properties. Before proceeding with them:
Lemma 1: Given an orthogonal polynomial sequence 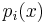 , any nth-degree polynomial S(x) can be expanded in terms of
, any nth-degree polynomial S(x) can be expanded in terms of  . That is, there are coefficients
. That is, there are coefficients  such that
such that
Proof by mathematical induction. Choose 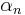 so that the
so that the 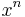 term of S(x) matches that of
term of S(x) matches that of 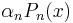 . Then
. Then 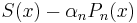 is an (n − 1)th-degree polynomial. Continue downward.
is an (n − 1)th-degree polynomial. Continue downward.
The coefficients  can be calculated directly using orthogonality. First multiply
can be calculated directly using orthogonality. First multiply  by
by 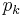 and weight function
and weight function 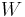 , then integrate:
, then integrate:
giving
Lemma 2: Given an orthogonal polynomial sequence, each of its polynomials is orthogonal to any polynomial of strictly lower degree.
Proof: Given n, any polynomial of degree n − 1 or lower can be expanded in terms of 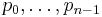 . Polynomial
. Polynomial 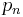 is orthogonal to each of them.
is orthogonal to each of them.
Minimal norm
Each polynomial in an orthogonal sequence has minimal norm among all polynomials with the same degree and leading coefficient.
Using orthogonality, the squared norm of p(x) satisfies
An interpretation of this result is that orthogonal polynomials are minimal in a generalized least squares sense. For example, the classical orthogonal polynomials have a minimal weighted mean square value.
Recurrence relations
Any orthogonal sequence has a recurrence formula relating any three consecutive polynomials in the sequence:
The coefficients a, b, and c depend on n, as well as the standardization.
We will prove this for fixed n, and omit the subscripts on a, b, and c.
First, choose a so that the 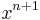 terms match, so we have
terms match, so we have
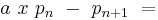 a polynomial of degree n.
a polynomial of degree n.
Next, choose b so that the 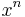 terms match, so we have
terms match, so we have
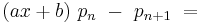 a polynomial of degree n − 1
a polynomial of degree n − 1
Expand the right-hand-side in terms of polynomials in the sequence
Now if 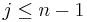 , then
, then
But
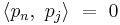 and
and 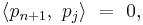
so
Since the inner product is just an integral involving the product:
we have
If 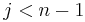 , then
, then 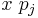 has degree
has degree 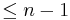 , so it is orthogonal to
, so it is orthogonal to 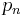 ; hence
; hence 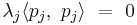 , which implies
, which implies 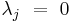 for
for 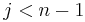 .
.
Therefore, only 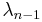 can be nonzero, so
can be nonzero, so
Letting 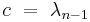 , we have
, we have
The values of 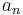 ,
, 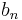 and
and  can be worked out directly. Let
can be worked out directly. Let 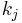 and
and 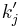 be the first and second coefficients of
be the first and second coefficients of 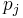 :
:
and 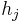 be the inner product of
be the inner product of 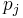 with itself:
with itself:
We have
Existence of real roots
Each polynomial in an orthogonal sequence has all n of its roots real, distinct, and strictly inside the interval of orthogonality.
This follows from the proof of interlacing of roots below. Here is a direct proof.
Let m be the number of places where the sign of Pn changes inside the interval of orthogonality, and let  be those points. Each of those points is a root of Pn. By the fundamental theorem of algebra, m ≤ n. Now m might be strictly less than n if some roots of Pn are complex, or not inside the interval of orthogonality, or not distinct. We will show that m = n.
be those points. Each of those points is a root of Pn. By the fundamental theorem of algebra, m ≤ n. Now m might be strictly less than n if some roots of Pn are complex, or not inside the interval of orthogonality, or not distinct. We will show that m = n.
Let 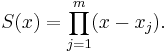
This is an mth-degree polynomial that changes sign at each of the xj, the same way that Pn(x) does. S(x)Pn(x) is therefore strictly positive, or strictly negative, everywhere except at the xj. S(x)Pn(x)W(x) is also strictly positive or strictly negative except at the xj and possibly the end points.
Therefore, 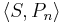 , the integral of this, is nonzero. But, by Lemma 2, Pn is orthogonal to any polynomial of lower degree, so the degree of S must be n.
, the integral of this, is nonzero. But, by Lemma 2, Pn is orthogonal to any polynomial of lower degree, so the degree of S must be n.
Interlacing of roots
The roots of each polynomial lie strictly between the roots of the next higher polynomial in the sequence.
First, standardize all of the polynomials so that their leading coefficients are positive. This will not affect the roots.
We use induction on n. Let n≥1 and let  be the roots of
be the roots of 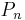 . Assuming by induction that the roots of
. Assuming by induction that the roots of 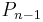 lie strictly between the
lie strictly between the 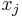 , we find that the signs of
, we find that the signs of 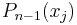 alternate with j. Moreover
alternate with j. Moreover 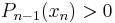 , since the leading coeffient is positive and
, since the leading coeffient is positive and 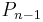 has no greater zero. To summarize,
has no greater zero. To summarize, 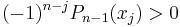 .
.
By the recurrence formula
with 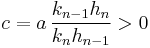 we conclude that
we conclude that 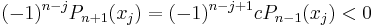 . By the intermediate value theorem,
. By the intermediate value theorem, 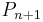 has at least one zero between
has at least one zero between 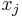 and
and 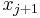 for
for  . Additionally,
. Additionally, 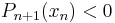 and the leading coefficient is posititive, so
and the leading coefficient is posititive, so 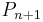 has an additional zero greater than
has an additional zero greater than 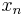 . For a similar reason it has a zero less than
. For a similar reason it has a zero less than  , and the induction step is complete.
, and the induction step is complete.
Differential equations leading to orthogonal polynomials
A very important class of orthogonal polynomials arises from a differential equation of the form
where Q is a given quadratic (at most) polynomial, and L is a given linear polynomial. The function f, and the constant λ, are to be found.
- (Note that it makes sense for such an equation to have a polynomial solution.
- Each term in the equation is a polynomial, and the degrees are consistent.)
This is a Sturm-Liouville type of equation. Such equations generally have singularities in their solution functions f except for particular values of λ. They can be thought of a eigenvector/eigenvalue problems: Letting D be the differential operator, 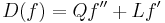 , and changing the sign of λ, the problem is to find the eigenvectors (eigenfunctions) f, and the corresponding eigenvalues λ, such that f does not have singularities and D(f) = λf.
, and changing the sign of λ, the problem is to find the eigenvectors (eigenfunctions) f, and the corresponding eigenvalues λ, such that f does not have singularities and D(f) = λf.
The solutions of this differential equation have singularities unless λ takes on specific values. There is a series of numbers 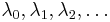 that lead to a series of polynomial solutions
that lead to a series of polynomial solutions 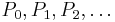 if one of the following sets of conditions are met:
if one of the following sets of conditions are met:
- Q is actually quadratic, L is linear, Q has two distinct real roots, the root of L lies strictly between the roots of Q, and the leading terms of Q and L have the same sign.
- Q is not actually quadratic, but is linear, L is linear, the roots of Q and L are different, and the leading terms of Q and L have the same sign if the root of L is less than the root of Q, or vice-versa.
- Q is just a nonzero constant, L is linear, and the leading term of L has the opposite sign of Q.
These three cases lead to the Jacobi-like, Laguerre-like, and Hermite-like polynomials, respectively.
In each of these three cases, we have the following:
- The solutions are a series of polynomials
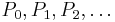 , each
, each 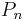 having degree n, and corresponding to a number
having degree n, and corresponding to a number 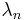 .
. - The interval of orthogonality is bounded by whatever roots Q has.
- The root of L is inside the interval of orthogonality.
- Letting
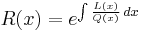 , the polynomials are orthogonal under the weight function
, the polynomials are orthogonal under the weight function 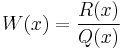
- W(x) has no zeros or infinities inside the interval, though it may have zeros or infinities at the end points.
- W(x) gives a finite inner product to any polynomials.
- W(x) can be made to be greater than 0 in the interval. (Negate the entire differential equation if necessary so that Q(x) > 0 inside the interval.)
Because of the constant of integration, the quantity R(x) is determined only up to an arbitrary positive multiplicative constant. It will be used only in homogeneous differential equations (where this doesn't matter) and in the definition of the weight function (which can also be indeterminate.) The tables below will give the "official" values of R(x) and W(x).
Rodrigues' formula
Under the assumptions of the preceding section, Pn(x) is proportional to ![\frac{1}{W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b448d8a0d17c7a845cc6f390072dfe95.png)
This is known as Rodrigues' formula, after Olinde Rodrigues. It is often written
where the numbers en depend on the standardization. The standard values of en will be given in the tables below.
The numbers λn
Under the assumptions of the preceding section, we have
(Since Q is quadratic and L is linear, 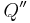 and
and  are constants, so these are just numbers.)
are constants, so these are just numbers.)
Second form for the differential equation
Let 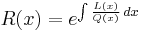 .
.
Then
Now multiply the differential equation
by R/Q, getting
or
This is the standard Sturm-Liouville form for the equation.
Third form for the differential equation
Let 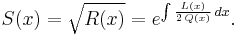
Then
Now multiply the differential equation
by S/Q, getting
or
But 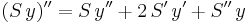 , so
, so
or, letting u = Sy,
Formulas involving derivatives
Under the assumptions of the preceding section, let ![P_n^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c0875bbb4d9f6694cfcffb850c4b83b.png) denote the rth derivative of
denote the rth derivative of 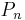 . (We put the "r" in brackets to avoid confusion with an exponent.)
. (We put the "r" in brackets to avoid confusion with an exponent.) ![P_n^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c0875bbb4d9f6694cfcffb850c4b83b.png) is a polynomial of degree n − r. Then we have the following:
is a polynomial of degree n − r. Then we have the following:
- (orthogonality) For fixed r, the polynomial sequence
![P_r^{[r]}, P_{r+1}^{[r]}, P_{r+2}^{[r]}, \dots](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7ef17a16c09c133e8d2668a12c4ecdd3.png) are orthogonal, weighted by
are orthogonal, weighted by 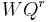 .
. - (generalized Rodrigues' formula)
![P_n^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c0875bbb4d9f6694cfcffb850c4b83b.png) is proportional to
is proportional to ![\frac{1}{W(x)[Q(x)]^r} \ \frac{d^{n-r}}{dx^{n-r}}\left(W(x)[Q(x)]^n\right)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/65392ae26ab14a970318ed5c3bc07191.png) .
. - (differential equation)
![P_n^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c0875bbb4d9f6694cfcffb850c4b83b.png) is a solution of
is a solution of ![{Q}\,y'' + (rQ'+L)\,y' + [{\lambda}_n-{\lambda}_r]\,y = 0\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8a4000406fce5167dd6b90c77aedb7e5.png) , where
, where 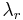 is the same function as
is the same function as 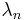 , that is,
, that is, 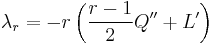
- (differential equation, second form)
![P_n^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/3c0875bbb4d9f6694cfcffb850c4b83b.png) is a solution of
is a solution of ![(RQ^{r}y')' + [{\lambda}_n-{\lambda}_r]RQ^{r-1}\,y = 0\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e19d69eaf0b2f0d0fdcd62956e609810.png)
There are also some mixed recurrences. In each of these, the numbers a, b, and c depend on n and r, and are unrelated in the various formulas.
There are an enormous number of other formulas involving orthogonal polynomials in various ways. Here is a tiny sample of them, relating to the Chebyshev, associated Laguerre, and Hermite polynomials:
Orthogonality
The differential equation for a particular λ may be written (omitting explicit dependence on x)
multiplying by 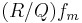 yields
yields
and reversing the subscripts yields
subtracting and integrating:
but it can be seen that
so that:
If the polynomials f are such that the term on the left is zero, and 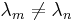 for
for 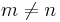 , then the orthogonality relationship will hold:
, then the orthogonality relationship will hold:
for 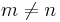 .
.
The classical orthogonal polynomials
The class of polynomials arising from the differential equation described above have many important applications in such areas as mathematical physics, interpolation theory, the theory of random matrices, computer approximations, and many others. All of these polynomial sequences are equivalent, under scaling and/or shifting of the domain, and standardizing of the polynomials, to more restricted classes. Those restricted classes are the "classical orthogonal polynomials".
- Every Jacobi-like polynomial sequence can have its domain shifted and/or scaled so that its interval of orthogonality is [−1, 1], and has Q = 1 − x2. They can then be standardized into the Jacobi polynomials
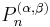 . There are several important subclasses of these: Gegenbauer, Legendre, and two types of Chebyshev.
. There are several important subclasses of these: Gegenbauer, Legendre, and two types of Chebyshev. - Every Laguerre-like polynomial sequence can have its domain shifted, scaled, and/or reflected so that its interval of orthogonality is
 , and has Q = x. They can then be standardized into the Associated Laguerre polynomials
, and has Q = x. They can then be standardized into the Associated Laguerre polynomials 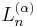 . The plain Laguerre polynomials
. The plain Laguerre polynomials 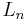 are a subclass of these.
are a subclass of these. - Every Hermite-like polynomial sequence can have its domain shifted and/or scaled so that its interval of orthogonality is
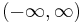 , and has Q = 1 and L(0) = 0. They can then be standardized into the Hermite polynomials
, and has Q = 1 and L(0) = 0. They can then be standardized into the Hermite polynomials 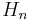 .
.
Because all polynomial sequences arising from a differential equation in the manner described above are trivially equivalent to the classical polynomials, the actual classical polynomials are always used.
Jacobi polynomials
The Jacobi-like polynomials, once they have had their domain shifted and scaled so that the interval of orthogonality is [−1, 1], still have two parameters to be determined. They are 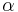 and
and 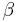 in the Jacobi polynomials, written
in the Jacobi polynomials, written 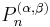 . We have
. We have 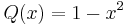 and
and  . Both
. Both 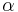 and
and 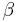 are required to be greater than −1. (This puts the root of L inside the interval of orthogonality.)
are required to be greater than −1. (This puts the root of L inside the interval of orthogonality.)
When 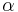 and
and 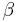 are not equal, these polynomials are not symmetrical about x = 0.
are not equal, these polynomials are not symmetrical about x = 0.
The differential equation
is Jacobi's equation.
For further details, see Jacobi polynomials.
Gegenbauer polynomials
When one sets the parameters 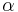 and
and 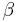 in the Jacobi polynomials equal to each other, one obtains the Gegenbauer or ultraspherical polynomials. They are written
in the Jacobi polynomials equal to each other, one obtains the Gegenbauer or ultraspherical polynomials. They are written 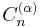 , and defined as
, and defined as
We have 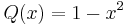 and
and 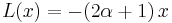 .
. 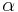 is required to be greater than −1/2.
is required to be greater than −1/2.
(Incidentally, the standardization given in the table below would make no sense for α = 0 and n ≠ 0, because it would set the polynomials to zero. In that case, the accepted standardization sets 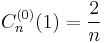 instead of the value given in the table.)
instead of the value given in the table.)
Ignoring the above considerations, the parameter 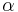 is closely related to the derivatives of
is closely related to the derivatives of 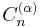 :
:
or, more generally:
All the other classical Jacobi-like polynomials (Legendre, etc.) are special cases of the Gegenbauer polynomials, obtained by choosing a value of 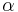 and choosing a standardization.
and choosing a standardization.
For further details, see Gegenbauer polynomials.
Legendre polynomials
The differential equation is
This is Legendre's equation.
The second form of the differential equation is:
The recurrence relation is
A mixed recurrence is
Rodrigues' formula is
For further details, see Legendre polynomials.
Associated Legendre polynomials
The Associated Legendre polynomials, denoted 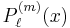 where
where 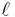 and
and  are integers with
are integers with 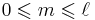 , are defined as
, are defined as
The m in parentheses (to avoid confusion with an exponent) is a parameter. The m in brackets denotes the mth derivative of the Legendre polynomial.
These "polynomials" are misnamed -- they are not polynomials when m is odd.
They have a recurrence relation:
For fixed m, the sequence 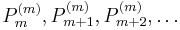 are orthogonal over [−1, 1], with weight 1.
are orthogonal over [−1, 1], with weight 1.
For given m, 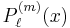 are the solutions of
are the solutions of
Chebyshev polynomials
The differential equation is
This is Chebyshev's equation.
The recurrence relation is
Rodrigues' formula is
These polynomials have the property that, in the interval of orthogonality,
(To prove it, use the recurrence formula.)
This means that all their local minima and maxima have values of −1 and +1, that is, the polynomials are "level". Because of this, expansion of functions in terms of Chebyshev polynomials is sometimes used for polynomial approximations in computer math libraries.
Some authors use versions of these polynomials that have been shifted so that the interval of orthogonality is [0, 1] or [−2, 2].
There are also Chebyshev polynomials of the second kind, denoted 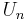
We have:
For further details, including the expressions for the first few polynomials, see Chebyshev polynomials.
Laguerre polynomials
The most general Laguerre-like polynomials, after the domain has been shifted and scaled, are the Associated Laguerre polynomials (also called Generalized Laguerre polynomials), denoted 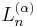 . There is a parameter
. There is a parameter 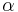 , which can be any real number strictly greater than −1. The parameter is put in parentheses to avoid confusion with an exponent. The plain Laguerre polynomials are simply the
, which can be any real number strictly greater than −1. The parameter is put in parentheses to avoid confusion with an exponent. The plain Laguerre polynomials are simply the 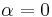 version of these:
version of these:
The differential equation is
This is Laguerre's equation.
The second form of the differential equation is
The recurrence relation is
Rodrigues' formula is
The parameter 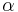 is closely related to the derivatives of
is closely related to the derivatives of 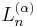 :
:
or, more generally:
Laguerre's equation can be manipulated into a form that is more useful in applications:
is a solution of
This can be further manipulated. When 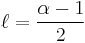 is an integer, and
is an integer, and 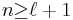 :
:
is a solution of
The solution is often expressed in terms of derivatives instead of associated Laguerre polynomials:
This equation arises in quantum mechanics, in the radial part of the solution of the Schrödinger equation for a one-electron atom.
Physicists often use a definition for the Laguerre polynomials that is larger, by a factor of 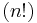 , than the definition used here.
, than the definition used here.
For further details, including the expressions for the first few polynomials, see Laguerre polynomials.
Hermite polynomials
The differential equation is
This is Hermite's equation.
The second form of the differential equation is
The third form is
The recurrence relation is
Rodrigues' formula is
The first few Hermite polynomials are
One can define the associated Hermite functions
Because the multiplier is proportional to the square root of the weight function, these functions are orthogonal over 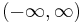 with no weight function.
with no weight function.
The third form of the differential equation above, for the associated Hermite functions, is
The associated Hermite functions arise in many areas of mathematics and physics. In quantum mechanics, they are the solutions of Schrödinger's equation for the harmonic oscillator. They are also eigenfunctions (with eigenvalue (−i)n) of the continuous Fourier transform.
Many authors, particularly probabilists, use an alternate definition of the Hermite polynomials, with a weight function of 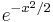 instead of
instead of 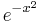 . If the notation He is used for these Hermite polynomials, and H for those above, then these may be characterized by
. If the notation He is used for these Hermite polynomials, and H for those above, then these may be characterized by
For further details, see Hermite polynomials.
Constructing orthogonal polynomials by the Gram–Schmidt process
The Gram–Schmidt process is an algorithm originally taken from linear algebra which removes linear dependency from a set of given vectors in an inner product space. The inner product as defined on all polynomials allows us to apply the Gram–Schmidt process to an arbitrary set of polynomials. The process removes linear dependencies from the polynomials, yielding sets of orthogonal polynomials. Given various initial polynomial sequences and weighting functions, different orthogonal polynomial sequences can be produced.
We define a projection operator on the polynomials as:
To apply the algorithm, we define our set of original polynomials 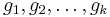 and generate a sequence of orthogonal polynomials
and generate a sequence of orthogonal polynomials 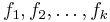 using:
using:
If an orthonormal sequence is required, a polynomial normalization operation can be defined as:
Care must be taken if the process is implemented on computer as the Gram–Schmidt process is numerically unstable. However, as many computational platforms implement rational numbers with arbitrary-precision arithmetic the problem can often be easily avoided.
Constructing orthogonal polynomials by using moments
Let
be the moments of a measure μ. Then the polynomial sequence defined by
is a sequence of orthogonal polynomials with respect to the measure μ. To see this, consider the inner product of pn(x) with xk for any k < n. We will see that the value of this inner product is zero[2].
(The entry-by-entry integration merely says the integral of a linear combination of functions is the same linear combination of the separate integrals. It is a linear combination because only one row contains non-scalar entries.)
Thus pn(x) is orthogonal to xk for all k < n. That means this is a sequence of orthogonal polynomials for the measure μ.
Table of classical orthogonal polynomials
| Name, and conventional symbol | Chebyshev, 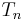 |
Chebyshev (second kind), 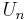 |
Legendre, 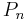 |
Hermite, 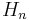 |
|---|---|---|---|---|
| Limits of orthogonality | 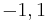 |
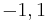 |
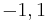 |
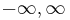 |
Weight, 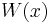 |
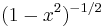 |
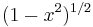 |
 |
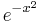 |
| Standardization | 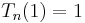 |
 |
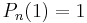 |
Lead term = 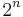 |
Square of norm, 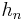 |
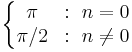 |
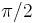 |
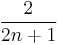 |
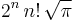 |
Leading term, 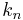 |
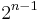 |
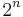 |
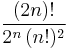 |
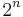 |
Second term, 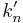 |
 |
 |
 |
 |
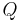 |
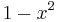 |
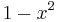 |
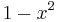 |
 |
 |
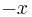 |
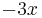 |
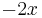 |
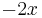 |
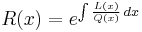 |
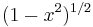 |
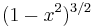 |
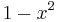 |
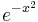 |
Constant in diff. equation, 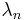 |
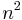 |
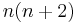 |
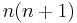 |
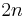 |
Constant in Rodrigues' formula, 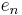 |
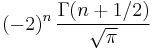 |
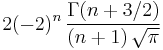 |
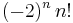 |
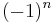 |
Recurrence relation, 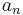 |
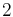 |
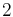 |
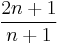 |
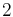 |
Recurrence relation, 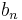 |
 |
 |
 |
 |
Recurrence relation, 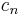 |
 |
 |
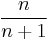 |
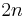 |
| Name, and conventional symbol | Associated Laguerre, 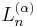 |
Laguerre, 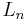 |
|---|---|---|
| Limits of orthogonality | 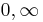 |
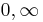 |
Weight, 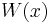 |
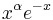 |
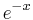 |
| Standardization | Lead term = 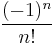 |
Lead term = 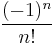 |
Square of norm, 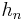 |
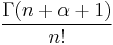 |
 |
Leading term, 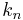 |
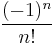 |
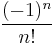 |
Second term, 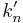 |
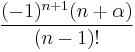 |
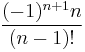 |
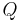 |
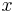 |
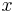 |
 |
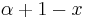 |
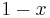 |
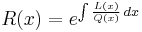 |
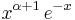 |
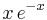 |
Constant in diff. equation, 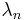 |
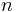 |
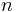 |
Constant in Rodrigues' formula, 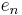 |
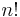 |
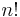 |
Recurrence relation, 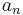 |
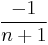 |
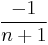 |
Recurrence relation, 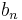 |
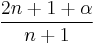 |
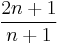 |
Recurrence relation, 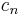 |
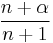 |
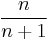 |
| Name, and conventional symbol | Gegenbauer, 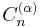 |
Jacobi, 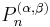 |
|---|---|---|
| Limits of orthogonality | 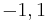 |
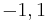 |
Weight, 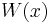 |
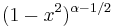 |
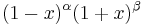 |
| Standardization | 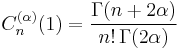 if if 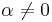 |
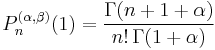 |
Square of norm, 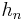 |
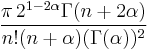 |
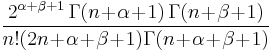 |
Leading term, 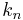 |
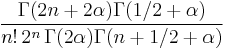 |
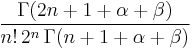 |
Second term, 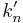 |
 |
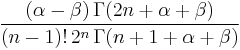 |
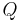 |
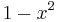 |
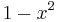 |
 |
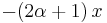 |
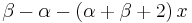 |
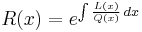 |
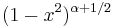 |
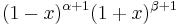 |
Constant in diff. equation, 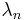 |
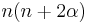 |
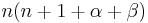 |
Constant in Rodrigues' formula, 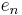 |
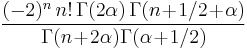 |
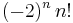 |
Recurrence relation, 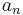 |
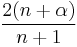 |
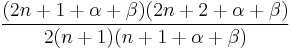 |
Recurrence relation, 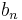 |
 |
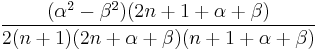 |
Recurrence relation, 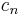 |
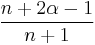 |
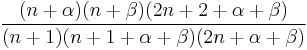 |
See also
- Polynomial sequences of binomial type
- Generalized Fourier series
- Sheffer sequence
- Appell sequence
- Umbral calculus
- Secondary measure
Notes
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 22", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 773, MR0167642, ISBN 978-0486612720, http://www.math.sfu.ca/~cbm/aands/page_773.htm.
- Gabor Szego (1939). Orthogonal Polynomials. Colloquium Publications - American Mathematical Society. ISBN 0-8218-1023-5.
- Dunham Jackson (1941, 2004). Fourier Series and Orthogonal Polynomials. New York: Dover. ISBN 0-486-43808-2.
- Refaat El Attar (2006). Special Functions and Orthogonal Polynomials. Lulu Press, Morrisville NC 27560. ISBN 1-4116-6690-9.
- Theodore Seio Chihara (1978). An Introduction to Orthogonal Polynomials. Gordon and Breach, New York. ISBN 0-677-04150-0.
Further reading
- Ismail, Mourad E. H. (2005). Classical and Quantum Orthogonal Polynomials in One Variable. Cambridge: Cambridge Univ. Press. ISBN 0-521-78201-5. http://www.cambridge.org/us/catalogue/catalogue.asp?isbn=9780521782012.
- Vilmos Totik (2005). "Orthogonal Polynomials". Surveys in Approximation Theory 1: 70–125. http://arxiv.org/abs/math.CA/0512424.
- Y.Z.Huang and Y.J.Long (2007). "On orthogonal polynomial approximation with the dimensional expanding technique for precise time integration in transient analysis". Communications in Nonlinear Science and Numerical Simulation 12: 1584–1603. doi:10.1016/j.cnsns.2006.03.007. http://pages.cs.wisc.edu/~huangyz/CNSNS07_Huang.pdf.
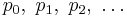
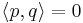
![W�: [x_1, x_2] \to \mathbb{R}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/498f89621f7dcdd7cd6af528ddfc1bdc.png)
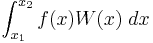
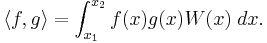
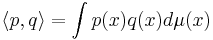
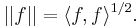
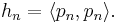
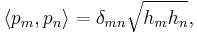
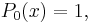
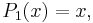
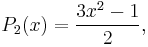
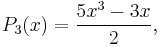
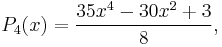

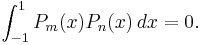
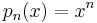
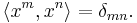
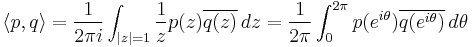
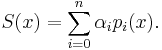
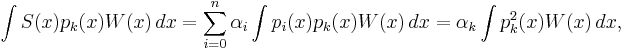
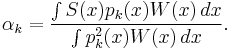
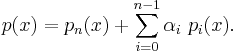
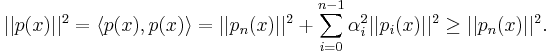
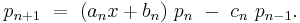
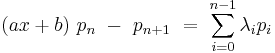
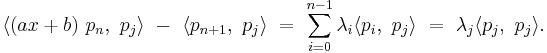
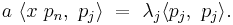
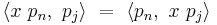
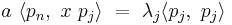
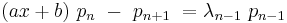
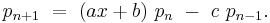
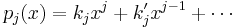
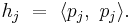
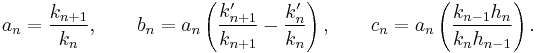
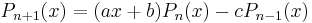
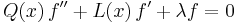
![P_n(x) = \frac{1}{{e_n}W(x)} \ \frac{d^n}{dx^n}\left(W(x)[Q(x)]^n\right)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/053c6bdce2a23cedd8699f20a10268e3.png)
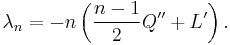
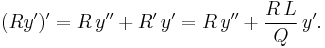
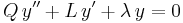
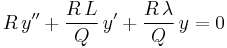
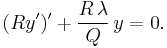
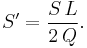
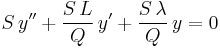
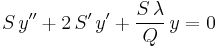
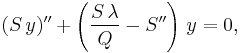
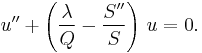
![P_n^{[r]} = aP_{n+1}^{[r+1]} + bP_n^{[r+1]} + cP_{n-1}^{[r+1]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9fedaa3a5585fc72cde284cae54bb210.png)
![P_n^{[r]} = (ax+b)P_n^{[r+1]} + cP_{n-1}^{[r+1]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6fc0ca2e6a38af7ca5f0bc4b10b573ea.png)
![QP_n^{[r+1]} = (ax+b)P_n^{[r]} + cP_{n-1}^{[r]}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/a0fd3dcf751f82f073dbd67b39202e6d.png)
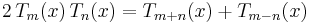
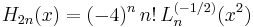
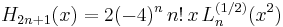
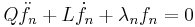
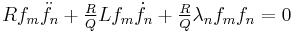
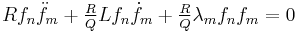
![\int_a^b \left[R(f_m\ddot{f}_n-f_n\ddot{f}_m)+
\textstyle\frac{R}{Q}L(f_m\dot{f}_n-f_n\dot{f}_m)\right] \, dx
+(\lambda_n-\lambda_m)\int_a^b \textstyle\frac{R}{Q}f_mf_n \, dx = 0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8f47296f1a5ee7edf3bc8b0e1ed1b9cc.png)
![\frac{d}{dx}\left[R(f_m\dot{f}_n-f_n\dot{f}_m)\right]=
R(f_m\ddot{f}_n-f_n\ddot{f}_m)\,\,+\,\,R\textstyle\frac{L}{Q}(f_m\dot{f}_n-f_n\dot{f}_m)](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4331ea50a455245c6864c0a8ca5ea9f5.png)
![\left[R(f_m\dot{f}_n-f_n\dot{f}_m)\right]_a^b\,\,+\,\,(\lambda_n-\lambda_m)\int_a^b \textstyle\frac{R}{Q}f_mf_n \, dx=0](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d23da4603e766dacae6cad1e540cebda.png)
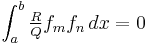
![(1-x^2)\,y'' + (\beta-\alpha-[\alpha+\beta+2]\,x)\,y' + {\lambda}\,y = 0\qquad \mathrm{with}\qquad\lambda = n(n+1+\alpha+\beta)\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/1321503a05a3b104841ee23b3c85dd81.png)
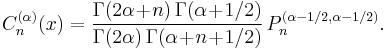
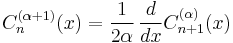
![C_n^{(\alpha+m)}(x) = \frac{\Gamma(\alpha)}{2^m\Gamma(\alpha+m)}\! \ C_{n+m}^{(\alpha)[m]}(x).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/5336d7784487eaada600bd1a550671a1.png)
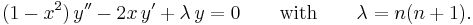
![([1-x^2]\,y')' + \lambda\,y = 0.\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/349c71aefe5ded586765655fc86f2080.png)
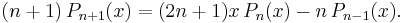
![P_{n+1}^{[r+1]}(x) = P_{n-1}^{[r+1]}(x) + (2n+1)\,P_n^{[r]}(x).\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d630f38abc3781bb57729ae8c4bce3de.png)
![P_n(x) = \,\frac{1}{2^n\,n!} \ \frac{d^n}{dx^n}\left([x^2-1]^n\right).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/da4878df654aff2cf0de4842e93b27ab.png)
![P_\ell^{(m)}(x) = (-1)^m\,(1-x^2)^{m/2}\ P_\ell^{[m]}(x).\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e9fd5a2e6ea03cb2beb863b02a69ba74.png)
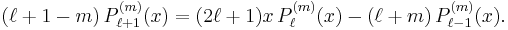
![(1-x^2)\,y'' -2xy' + \left[\lambda - \frac{m^2}{1-x^2}\right]\,y = 0\qquad \mathrm{with}\qquad\lambda = \ell(\ell+1).\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/e61264ba79b18b37aa1812d7190ca448.png)
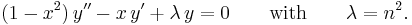
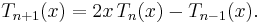
![T_n(x) = \frac{\Gamma(1/2)\sqrt{1-x^2}}{(-2)^n\,\Gamma(n+1/2)} \ \frac{d^n}{dx^n}\left([1-x^2]^{n-1/2}\right).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9e12b85879596322a888ca2562cf9d43.png)
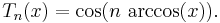
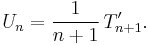
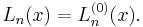
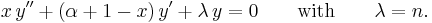
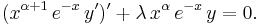
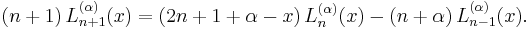
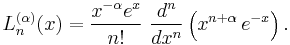
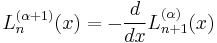
![L_n^{(\alpha+m)}(x) = (-1)^m L_{n+m}^{(\alpha)[m]}(x).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/7cfc4e6e0c5850b0130370b7f22f20ee.png)
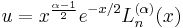
![u'' + \frac{2}{x}\,u' + \left[\frac{\lambda}{x} - \frac{1}{4} - \frac{\alpha^2-1}{4x^2}\right]\,u = 0\qquad \mathrm{with}\qquad\lambda = n+\frac{\alpha+1}{2}.\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b9c721c43b29ce67936da4069b68f806.png)
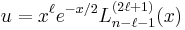
![u'' + \frac{2}{x}\,u' + \left[\frac{\lambda}{x} - \frac{1}{4} - \frac{\ell(\ell+1)}{x^2}\right]\,u = 0\text{ with }\lambda = n.\,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/4e3e322420e5d87e7bdbf96cc1688ec5.png)
![u = x^{\ell}e^{-x/2}L_{n+\ell}^{[2\ell+1]}(x).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/2b599d0ea83a7779385e5da70029ce04.png)
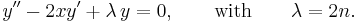
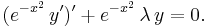
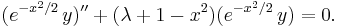
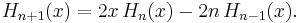
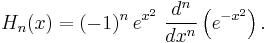





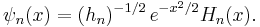
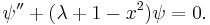
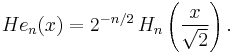
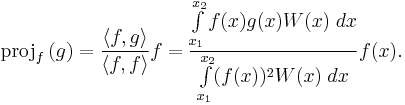
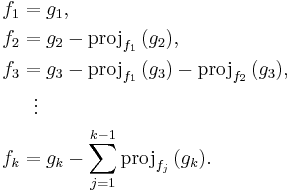
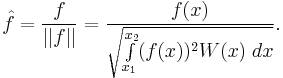
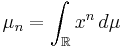
![p_n(x) = \det\left[
\begin{matrix}
\mu_0 & \mu_1 & \mu_2 & \cdots & \mu_n \\
\mu_1 & \mu_2 & \mu_3 & \cdots & \mu_{n+1} \\
\mu_2 & \mu_3 & \mu_4 & \cdots & \mu_{n+2} \\
\vdots & \vdots & \vdots & & \vdots \\
\mu_{n-1} & \mu_n & \mu_{n+1} & \cdots & \mu_{2n-1} \\
1 & x & x^2 & \cdots & x^n
\end{matrix}
\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/0186d9076b55a62ce10c57dde7c024f3.png)
![\begin{align}
\int_\mathbb{R} x^k p_n(x)\,d\mu
& {} = \int_\mathbb{R} x^k \det\left[
\begin{matrix}
\mu_0 & \mu_1 & \mu_2 & \cdots & \mu_n \\
\mu_1 & \mu_2 & \mu_3 & \cdots & \mu_{n+1} \\
\mu_2 & \mu_3 & \mu_4 & \cdots & \mu_{n+2} \\
\vdots & \vdots & \vdots & & \vdots \\
\mu_{n-1} & \mu_n & \mu_{n+1} & \cdots & \mu_{2n-1} \\
1 & x & x^2 & \cdots & x^n
\end{matrix} \right]
\,d\mu \\ \\
& {} = \int_\mathbb{R} \det\left[
\begin{matrix}
\mu_0 & \mu_1 & \mu_2 & \cdots & \mu_n \\
\mu_1 & \mu_2 & \mu_3 & \cdots & \mu_{n+1} \\
\mu_2 & \mu_3 & \mu_4 & \cdots & \mu_{n+2} \\
\vdots & \vdots & \vdots & & \vdots \\
\mu_{n-1} & \mu_n & \mu_{n+1} & \cdots & \mu_{2n-1} \\
x^k & x^{k+1} & x^{k+2} & \cdots & x^{k+n}
\end{matrix} \right]
\,d\mu \\ \\
& {} = \det\left[
\begin{matrix}
\mu_0 & \mu_1 & \mu_2 & \cdots & \mu_n \\
\mu_1 & \mu_2 & \mu_3 & \cdots & \mu_{n+1} \\
\mu_2 & \mu_3 & \mu_4 & \cdots & \mu_{n+2} \\
\vdots & \vdots & \vdots & & \vdots \\
\mu_{n-1} & \mu_n & \mu_{n+1} & \cdots & \mu_{2n-1} \\
\displaystyle \int_\mathbb{R} x^k \, d\mu & \displaystyle \int_\mathbb{R} x^{k+1} \, d\mu & \displaystyle \int_\mathbb{R} x^{k+2} \, d\mu & \cdots & \displaystyle \int_\mathbb{R} x^{k+n} \, d\mu
\end{matrix} \right] \\ \\
& {} = \det \left[
\begin{matrix}
\mu_0 & \mu_1 & \mu_2 & \cdots & \mu_n \\
\mu_1 & \mu_2 & \mu_3 & \cdots & \mu_{n+1} \\
\mu_2 & \mu_3 & \mu_4 & \cdots & \mu_{n+2} \\
\vdots & \vdots & \vdots & & \vdots \\
\mu_{n-1} & \mu_n & \mu_{n+1} & \cdots & \mu_{2n-1} \\
\mu_k & \mu_{k+1} & \mu_{k+2} & \cdots & \mu_{k+n}
\end{matrix} \right] \\ \\
& {} = 0\text{ if } k < n,\text{ since the matrix has two identical rows}.
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/8226237a06b7af660fa3e6ef6ad2f74f.png)